This quick-start tutorial demonstrates how to configure the Decision Support System and simulate its use. The example involves artificial and easily comprehensible data. The modelled decision-making process makes the following assumptions:
- A simple 2D decision problem is considered.
- The process is modelled as interactive.
- The process involves a robust preference learning strategy, named ERS (http://ssrn.com/abstract=5415565).
- The decision maker’s preferences are assumed to be consistent with an L-norm.
- The interactive procedure randomly selects two pairs of solutions to be presented to the decision-maker for evaluation.
- The decision maker’s responses are simulated using an artificial decision maker, consistent with the L-norm.
The results of the processing are visualized and reported in the console. Note that, although it is a quick-start tutorial, having at least a moderate understanding of the concepts described in “Tutorial Series on Java Framework for Evolutionary Computation and Decision Making. Tutorial 4: Decision Support module” is recommended. The complete source code for this tutorial can be found in the Projects module: y2025.SoftwareX_JECDM.QuickStart1 (framework’s version at least 1.7.0). In what follows, the relevant commented code blocks are presented, and the expected results are visualized for convenience. Note that a list of essential imports can be found at the end of this tutorial.
The overview of the source code:
The code starts by defining three elements:
1) random number generator,
2) considered criteria
3) normalization functions mapping the considered objective space into a normalized hypercube:
// Let us start with defining a random number generator:
IRandom R = new L32_X64_MIX(0);
// Then, we can proceed to define two criteria, named C1 and C2. The first is of the cost-type, while the latter is of the gain-type.
Criteria C = Criteria.constructCriteria(
new String[]{"C1", "C2"}, // criteria names
new boolean[]{false, true} // criteria types (false = cost; true = gain)
);
// We will also assume that the alternatives are spanned on the [0, 10] interval for the first criterion, and on the [1, 2] interval for the latter. Important: the scaling-sensitive components assume that the calculations are performed in the [0, 1] hypercube, with the 0-vector being the utopia and 1-vector the nadir, by default. Thus, we need to define suitable normalization functions that will be passed to these components to allow them to perform adequate rescaling:
INormalization[] normalizations = new INormalization[]{
new Linear(0.0d, 10.0d), // Linear = performs standard min-max rescaling (min = 0, max = 10)
new LinearWithFlip(1.0d, 2.0d, 1.0d) // LinearWithFlip = as Linear, but flips the
// normalization product around the passed threshold, i.e., final normalization = 1 - normalization. Flipping is required as the second criterion is of the gain-type.
};Code language: JavaScript (javascript)Then, a set of artificial alternatives is generated:
// Now, assume an artificial set of alternatives whose performance vectors are defined on a 2-dimensional concave sphere that is suitably rescaled to account for the expected performance bounds and criteria types. We will first construct the relevant performance matrix (alternatives x performances) using the standard parametric equation of a sphere:
int noAlternatives = 50; // the number of alternatives in the artificial data set
double[][] pm = new double[noAlternatives][2];
for (int i = 0; i < noAlternatives; i++)
{
double angle = Math.PI / 2.0d * (double) i / (noAlternatives - 1);
pm[i][0] = Math.sin(angle) * 10.0d; // performance according to the first criterion (cost, [0, 10] bound)
pm[i][1] = 2.0d - Math.cos(angle); // performance according to the second criterion (gain, [1, 2] bound)
}
// We can now define an alternative set using the performance matrix. The resulting alternatives will be named "A1", "A2", and so on.
Alternatives alternatives = Alternatives.getAlternativeArray("A", pm, 1);
// Let us print the data on alternatives:
assert alternatives != null;
for (Alternative A : alternatives)
System.out.println(A.getName() + " : "
+ PrintUtils.getVectorOfDoubles(A.getPerformanceVector(), 2).replace(',', '.'));Code language: JavaScript (javascript)The following code starts configuring the decision support system. This process begins by defining a refiner object, used to pre-process the input alternatives:
// We will start by constructing a decision-support system. It requires a considerable amount of
// parameterization, which can be done via the inner Params class:
DecisionSupportSystem.Params pDSS = new DecisionSupportSystem.Params();
pDSS._criteria = C; // defined the criteria
{
// Refiner is an object that pre-processes input alternatives used when running the system. It involves
// checking the premature termination criteria (optional). If none of them is triggered, the system
// proceeds to perform an optional reduction step using reduction filters. They intend to filter out
// unwanted input alternatives.
Refiner.Params pR = new Refiner.Params(); // to be parameterized via the Params class
pR._terminationFilters = new LinkedList<>(); // define the termination filters
pR._terminationFilters.add(new RequiredSpread(1.0E-3)); // RequiredSpread: checks if the input
// alternatives are contained within a hypercube of the input size. The measurement is done in
// the normalized space. If so, it is assumed that the alternatives are too narrowly spread to make
// meaningful processing. Thus, the processing would be terminated.
pR._reductionFilters = new LinkedList<>(); // define the reduction filters
pR._reductionFilters.add(new RemoveDominated()); // RemoveDominated: removes dominated alternatives as they
// are rarely useful (important note, these filters sequentially create new alternative sets (in fact,
// arrays) and pass them further, the input set is not manipulated)
pDSS._refiner = new Refiner(pR); // instantiate the refiner
}Code language: PHP (php)Next, an interaction trigger that specifies an interaction pattern is defined:
// Let us now define an interaction trigger. It can accept a series of rules for checking if the preference elicitation should be performed when executing the processing. In this tutorial example, we assume that the rule is based on verifying the interaction counter. We will assume that interactions are allowed every 5 iterations, starting from the 10th iteration. A limit of 2 interactions is also imposed.
pDSS._interactionTrigger = new InteractionTrigger(
new IterationInterval( // rule based on examining the iteration counter
10, // allow for interactions starting from the 10th iteration
5, // allow for iterations every 5 iterations
2 // impose the limit of 2 iterations
)
);Code language: PHP (php)Then, a procedure for creating a reference subset of alternatives to be evaluated by the decision-maker is defined:
// Now, we need to establish a reference set constructor. "Reference Sets" is a subset of the input alternatives that serves as a foundation for preference elicitation. In this example, we assume that the elicitation is based on pairwise comparisons. For simplicity, we also assume that these pairs are selected randomly. The object allows for mapping different constructors to different Decision Makers. We assume cooperation with just one Decision Maker, named DM1.
{
ReferenceSetsConstructor.Params pRSC = new ReferenceSetsConstructor.Params(); // parameterize via the Params class
LinkedList<IReferenceSetConstructor> rsc = new LinkedList<>(); // instantiate a list of constructors
// RandomPairs: select a pair randomly (drawn from a uniform distribution). The input validator
// RequiredSpread sets neglecting pairs contained within a hypercube of size 10-3 (in the normalized space).
rsc.add(new RandomPairs(new interaction.reference.validator.RequiredSpread(1.0E-3)));
pRSC._dmConstructors = new HashMap<>();
// Map the constructors onto the Decision Maker labelled as DM1:
pRSC._dmConstructors.put("DM1", rsc);
// Instantiate the reference sets constructor:
pDSS._referenceSetsConstructor = new ReferenceSetsConstructor(pRSC);
}Code language: PHP (php)This tutorial assumes a cooperation with an artificial decision-maker, whose value system is modeled with an L-norm:
// We will now define a feedback provider. This object is responsible for creating feedback based on the input reference sets. We will use an artificial Decision Maker modelled with an L-norm. Specifically, when presenting a pair to be compared, the suitably configured feedback provider will use the model to verify which alternative is better by comparing the attained scores. An alternative that achieves a better score will be considered preferred:
{
// Define the artificial Decision Maker's model as the L-norm:
IPreferenceModel<LNorm> dmModel = new model.definitions.LNorm(
new LNorm(new double[]{0.6d, 0.4d}, // the weights
Double.POSITIVE_INFINITY, // the compensation level: makes the function effectively
// a Weighted Chebyshev function
INormalization.getCloned(normalizations) // normalizations used to rescale alternatives
// when making a comparison
));
// Create a single-DM feedback provider using the instantiated model. Note that the decision maker's label must match those defined when creating the reference sets constructor
pDSS._feedbackProvider = FeedbackProvider.getForSingleDM(
"DM1", new ArtificialValueDM<>(dmModel));
}Code language: PHP (php)Then, the code defines three core components related to learning preferences in the configured system:
1) the definition of the assumed preference model,
2) the preference learning algorithm,
3) and the inconsistency handler:
// Finally, we will define the data used to instantiate the decision maker's model system. This system is
// primarily responsible for handling the preference learning part. It comprises three elements: preference
// model definition, preference learning procedure, and inconsistency handler.
{
// We need to start by constructing a single model bundle that will be associated with the decision maker's bundle:
ModelBundle<LNorm> modelBundle = new ModelBundle<>();
// Assume that the model to be learned is defined as an L-Norm:
modelBundle._preferenceModel = new model.definitions.LNorm(
null, // null = no internal models, i.e., concrete instances, are supplied a priori):
// a dedicated evaluator may be bound with the preference model; for this reason, one may implement a suitable interface:
new IEvaluator<>()
{
[...]
@Override
public EvaluationResult evaluateAlternatives(AbstractAlternatives<?> alternatives, ArrayList<LNorm> models) throws PreferenceModelException
{
// We will implement this method to allow batch evaluation of the input alternatives
given the internal models (constructed instances). This example procedure assigns a score of 0 or 1 to
each alternative in accordance with the relation of potential optimality. Specifically, an alternative
is considered potentially optimal (i.e., the most relevant) if it achieves the highest score among other
alternatives for at least one compatible model instance. Such alternatives will be assigned a score of 1.
Otherwise, a score of 0 will be assigned. An auxiliary class PO (Potential Optimality) will be employed
to perform these calculations. Note that the procedure generates a complex result that involves the
processing time as well. The calculated scores are stored in an array (double []) whose elements match
the input alternatives 1:1 by index.
EvaluationResult evaluationResult = new EvaluationResult();
evaluationResult._startTime = System.nanoTime();
evaluationResult._evaluations = new double[alternatives.size()];
for (int i = 0; i < alternatives.size(); i++)
evaluationResult._evaluations[i] = PO.isHolding(alternatives.get(i), alternatives, models) ? 1.0d : 0.0d;
evaluationResult._elapsedTime = (long) ((System.nanoTime() - evaluationResult._startTime) / 1000000.0d);
return evaluationResult;
}
}
);
{
// The following code defines the preference learning strategy called each time a new feedback is
received. We will use the ERS procedure proposed in https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5415565.
This method generates a series of L-norm instances that (i) are compatible with the feedback and (ii) are evenly
spaced in the model parameter space.
ERS.Params<LNorm> pERS = new ERS.Params<>( // parameterize via the Params class
// an auxiliary random model generator must be delivered (this generator constructs random L-norms)
new LNormGenerator(
C._no, // the number of criteria
Double.POSITIVE_INFINITY)); // the compensation level (makes the model a weighted Chebyshev function)
pERS._similarity = new Euclidean(); // similarity measure (defines a similarity between two L-norms as
// a Euclidean distance between their weight vectors)
pERS._kMostSimilarNeighbors = 3;
pERS._feasibleSamplesToGenerate = 50; // the number of feasible models to generate
pERS._iterationsLimit = new Constant(100000); // the limit for the number of iterations for the ERS procedure
pERS._comparator = new MostSimilarWithTieResolving<>(); // model comparator (see the Java Doc description)
pERS._EMC = new EvolutionaryModelConstructor<>( // evolutionary model constructor; this object defines
// rules for generating a new model using parent ones (see the paper on ERS for more details)
new LNormOnSimplex(Double.POSITIVE_INFINITY, 0.2d, 0.2d),
new Tournament<>(2)
);
modelBundle._modelConstructor = new ERS<>(pERS); // instantiate the preference learning procedure
}
// Inconsistency handler is triggered when a preference learning procedure is not capable of constructing
// feasible models; RemoveOldest = removes the oldest feedback and runs the preference learning procedure
// until compatibility is restored. Then, starting from the newest removed models, these removed models
// are individually reintroduced to the feedback set as long as they do not violate the consistency.
modelBundle._inconsistencyHandler = new RemoveOldest<>();
// Finally, we can establish a decision maker's bundle associated with the decision maker labelled as DM1:
DMBundle dmBundle = new DMBundle("DM1", modelBundle);
pDSS._dmBundles = new DMBundle[]{dmBundle};
}Code language: Java (java)The following code instantiates the decision support system as defined above. Also, it prepares two plots that will be used to visualize the alternatives space along with the decision maker’s feedback, and the learnt preference model instances compatible with the feedback:
// We can now instantiate the suitably configured decision-support system. Note that the constructor can throw a custom exception during a thorough validation of the input.
try
{
DecisionSupportSystem DSS = new DecisionSupportSystem(pDSS);
// This notification must be executed before starting processing:
DSS.notifySystemStarts();
// For convenience, let us present the results twofold. First, we will use a regular 2D scatter plot to
// depict the objective/criteria space. It will illustrate (i) potentially optimal alternatives,
// (ii) not potentially optimal alternatives, and (iii) pairwise comparisons made by
// the artificial decision-maker.
Plot2D plotOS = Plot2DFactory.getPlot(
"f1", "f2", // axes' labels
DRMPFactory.getFor2D(new Range(0.0d, 10.0d), new Range(1.0d, 2.0d)), // axes' limits
5, 5, // the number of ticks for the axes
"0.00", // axes' tick label formatting
1.5f, // font rescalling factor
scheme -> scheme._colors.put(ColorFields.PLOT_BACKGROUND, Color.WHITE), // set the plot background color to white
pP -> pP._drawLegend = true // request drawing the legend
);
// Second, we will use another scatter plot to depict weight vectors of the compatible models learnt by ERS:
Plot2D plotWS = Plot2DFactory.getPlot(
"w1", "w2", // axes' labels
DRMPFactory.getFor2D(Range.getNormalRange(), Range.getNormalRange()), // axes' limits
5, 5, // the number of ticks for the axes
"0.00", // axes' tick label formatting
1.5f, // font rescalling factor
scheme -> scheme._colors.put(ColorFields.PLOT_BACKGROUND, Color.WHITE), // set the plot background color to white
pP -> pP._drawLegend = true // request drawing the legend
);
// Organize the plots in a grid (1 row, 2 columns):
GridPlots GP = new GridPlots(new AbstractPlot[]{plotOS, plotWS}, 1, 2);
// Construct the frame and display it:
Frame frame = new Frame(GP, 1600, 800);
frame.setVisible(true);Code language: JavaScript (javascript)Next, running the system is simulated in the loop. It communicates with external components via the decision-making context:
// In this example, we will iteratively run the system. If the preference elicitation and model update are triggered in an iteration, we will be deriving potentially optimal solutions. They will be stored in the PO object and passed to the system in the following iterations, subsequently reducing the number of alternatives for consideration. Here, we can treat the alternatives object explicitly as PO:
Alternatives PO = alternatives;
for (int it = 0; it < 30; it++) // the limit for the number of iterations = 30
{
System.out.println("Iteration = " + it + " ====================================");
// When running the system, a decision-making context must be specified and passed to the central method (context's params container). It bridges the system with some external components (e.g., an evolutionary algorithm for multiple objective optimization):
DMContext.Params pDMC = new DMContext.Params(); // create the context (params container)
pDMC._currentAlternativesSuperset = PO; // define the current set of alternatives
// Define the current objective (criteria) space bounds (utopia [0, 2] and nadir [10, 1] points are passed via the constructor):
pDMC._currentOS = new ObjectiveSpace(new double[]{0.0d, 2.0d}, new double[]{10.0d, 1.0d});
// The normalization builder is responsible for deriving normalization functions, properly rescaling the objective space into [0, 1] hypercube. The standard builder constructs regular linear normalization functions for the cost-type criteria, and linear normalization functions with a flip for the gain-type criteria
pDMC._normalizationBuilder = new StandardLinearBuilder();
// If this flag is set to true, the normalization functions are derived and propagated
// to relevant rescaling-sensitive objects:
pDMC._osChanged = true;
pDMC._currentIteration = it; // current iteration number
pDMC._R = R; // random number generator to be used in various system's components
// Having defined the context, we can call the "execute process" method. It first attempts to perform the preference elicitation. If it is performed successfully, it executes the preference learning procedures to discover the proper parameterization of the assumed preference models. The summary of the whole processing is returned in a complex Report object:
Report report = DSS.executeProcess(pDMC);Code language: PHP (php)For those interactions in which the interaction was triggered, the report on the processing is printed, and alternatives that are potentially optimal to the decision-maker are determined:
// If the preference elicitation was triggered (by default, it should happen in the 10th
// and 15th iterations):
// - we will print the report and other auxiliary information
// - we will update the plots
if (report._elicitationReport._interactionStatus.equals(Status.PROCESS_ENDED_SUCCESSFULLY))
{
report.printStringRepresentation(3); // print the report
// Print the decision maker's history of preference elicitation:
System.out.println("Preference elicitation history:");
History history = DSS.getDecisionMakersSystems()[0].getHistory();
System.out.println(history.getFullStringRepresentation());
// Evaluate the alternatives using the implemented evaluator:
EvaluationResult evaluationResult = DSS.getDecisionMakersSystems()[0].getModelSystems()[0].evaluateAlternatives(alternatives);
// Print the evaluation result:
System.out.println("Evaluation result:");
System.out.println(evaluationResult.toString());
// We can now determine the subset of alternatives that proved potentially optimal:
ArrayList<Alternative> aPO = new ArrayList<>(alternatives.size());
for (int i = 0; i < alternatives.size(); i++)
if (Double.compare(evaluationResult._evaluations[i], 0.5d) >= 0) aPO.add(alternatives.get(i));
// We will use these derived alternatives to instantiate a new PO object that will be passed via
// the context in subsequent iterations:
PO = new Alternatives(aPO);
System.out.println("Potentially optimal alternatives = " + PO.size());Code language: JavaScript (javascript)The following code updates the first plot depicting the objective space:
// The following code constructs data sets to be displayed on plot 1:
{
ArrayList<IDataSet> DSs = new ArrayList<>(); // define data sets array
// We will first focus on the pairwise comparisons. We will parse them from the history of
// preference elicitation and store them in an array of alternatives (each pair will be
// associated with one pairwise comparison):
ArrayList<Alternative> pcs = new ArrayList<>(history.getNoPreferenceExamples() * 2);
// Note that the history protects access to stored feedback.
// A copy of auxiliary wrappers can be retrieved, though:
for (PreferenceInformationWrapper piw : history.getPreferenceInformationCopy())
{
// Check the types and ignore irrelevant forms (should not happen in this example):
if (!(piw._preferenceInformation instanceof PairwiseComparison PC)) continue;
if (!PC.getRelation().equals(Relations.PREFERENCE)) continue;
// RRetrieve the alternatives and store them in the array (side note: the alternatives are
// not immutable; thus, the preference elicitation history is not completely immutable as well):
pcs.add(PC.getNotPreferredAlternative());
pcs.add(PC.getPreferredAlternative());
}
// Generate data matrix to be displayed:
double[][] data = new double[pcs.size()][2];
for (int i = 0; i < pcs.size(); i += 2)
{
data[i][0] = pcs.get(i).getPerformanceVector()[0];
data[i][1] = pcs.get(i).getPerformanceVector()[1];
data[i + 1][0] = pcs.get(i + 1).getPerformanceVector()[0];
data[i + 1][1] = pcs.get(i + 1).getPerformanceVector()[1];
}
// Create a data set to be illustrated as arrows reflecting the pairwise comparisons:
DSs.add(DSFactory2D.getDS(
"PCs", // data set name
data, // data (matrix)
new LineStyle(1.0f, color.gradient.Color.BLUE), // line style (width and color)
new ArrowStyles( // arrow style; an end of the arrow is defined:
new ArrowStyle( // style for the arrow's end
3.5f, // length
3.5f, // width
color.gradient.Color.BLUE, // fill color
Arrow.TRIANGULAR_2D // style
)
),
// Important flag for data interpretation: if true, each pair in the input data
// matrix will be treated as a singular and disconnected line (if false, the whole
// matrix will be assumed to contain a series of points forming a connected series of lines):
true
)
);
// The following lines prepare a data set portraying all alternatives:
data = new double[alternatives.size()][2];
for (int i = 0; i < alternatives.size(); i++)
{
data[i][0] = alternatives.get(i).getPerformanceVector()[0];
data[i][1] = alternatives.get(i).getPerformanceVector()[1];
}
DSs.add(DSFactory2D.getDS("All alternatives", data,
new MarkerStyle(
1.0f, // size
color.gradient.Color.RED, // fill color
Marker.CIRCLE, // style
2.0f // size used when drawing a corresponding legend entry
)));
// The following lines prepare a data set portraying potentially optimal alternatives:
data = new double[PO.size()][2];
for (int i = 0; i < PO.size(); i++)
{
data[i][0] = PO.get(i).getPerformanceVector()[0];
data[i][1] = PO.get(i).getPerformanceVector()[1];
}
DSs.add(DSFactory2D.getDS("PO alternatives", data,
new MarkerStyle(
2.0f, // size
color.gradient.Color.BLACK, // fill color
Marker.SQUARE, // style
3.0f // size used when drawing a corresponding legend entry
)));
// Update data sets:
plotOS.getModel().setDataSets(
DSs, true, // update the display ranges (prepares axes' titles, etc.)
true // update data associated with legend rendering
);
}Code language: PHP (php)The following code updates the first plot depicting the compatible model space, and creates a joint render to be stored on a disc:
// The following code constructs data sets to be displayed on plot 2 (compatible models' weight vectors):
{
// Derive the preference model:
IPreferenceModel<? extends AbstractInternalModel> preferenceModel =
DSS.getDecisionMakersSystems()[0].getModelSystems()[0].getPreferenceModel();
// Derive the model's instances:
ArrayList<? extends AbstractInternalModel> models = preferenceModel.getInternalModels();
// Prepare a data matrix associated with internal models' weight vectors:
double[][] w = new double[models.size()][2];
for (int i = 0; i < models.size(); i++)
w[i] = models.get(i).getWeights().clone(); // note that getWeights() method is imposed by
// the implemented interface; the result may vary depending on the concrete model definition;
// also the clone method is used for safety
// Create the data set and update the plot:
plotWS.getModel().setDataSet(DSFactory2D.getDS("Compatible weights", w,
new MarkerStyle(1.0f, // size
color.gradient.Color.BLACK, // fill color
Marker.SQUARE // style
)),
true, // update the display ranges (prepares axes' titles, etc.)
true // update data associated with legend rendering
);
}
// For this quick-start tutorial, the screenshot of the plot is generated and stored.
// It can be accomplished in the following way:
Screenshot screenshot1 = plotOS.getModel().requestScreenshotCreation(
plotOS.getWidth(), // screenshot width (independent to the current plot width)
plotOS.getHeight(), // screenshot height (independent to the current plot height)
false, // do not use the alpha channel
null // optional parameter that indicates that the plot will be clipped to its content by
// removing the first/last columns/rows that match the given color (e.g., check Color.WHITE)
);
// For this quick-start tutorial, the screenshot of the plot is generated and stored.
// It can be accomplished in the following way:
Screenshot screenshot2 = plotWS.getModel().requestScreenshotCreation(
plotWS.getWidth(), // screenshot width (independent to the current plot width)
plotWS.getHeight(), // screenshot height (independent to the current plot height)
false, // do not use the alpha channel
null // optional parameter that indicates that the plot will be clipped to its content by
// removing the first/last columns/rows that match the given color (e.g., check Color.WHITE)
);
screenshot1._barrier.await();
screenshot2._barrier.await();
BufferedImage screenshot = ImageUtils.mergeHorizontally(screenshot1._image, screenshot2._image);
// Finally, we can use the following method to save the screenshot.
ImageSaver.saveImage(
screenshot, // screenshot to be saved
"D:" + File.separatorChar + "quickstart3_" + it, // file path (excludes the extension; alter it according
// to your computer specification and needs)
"jpg", // file extension (only regular file types, e.g., bmp or jpg are supported; in the case of
// providing an unsupported extension, an error message will be printed)
1.0f // image quality (1.0 = the best; not all extensions support this parameter)
);
}
}
} catch (DecisionSupportSystemException | ModelSystemException | HistoryException | InterruptedException e)
{
throw new RuntimeException(e);
}Code language: PHP (php)An example console output associated with the report on the system’s processing done in the 15th iteration (when the second interaction was expected to happen) is illustrated below:
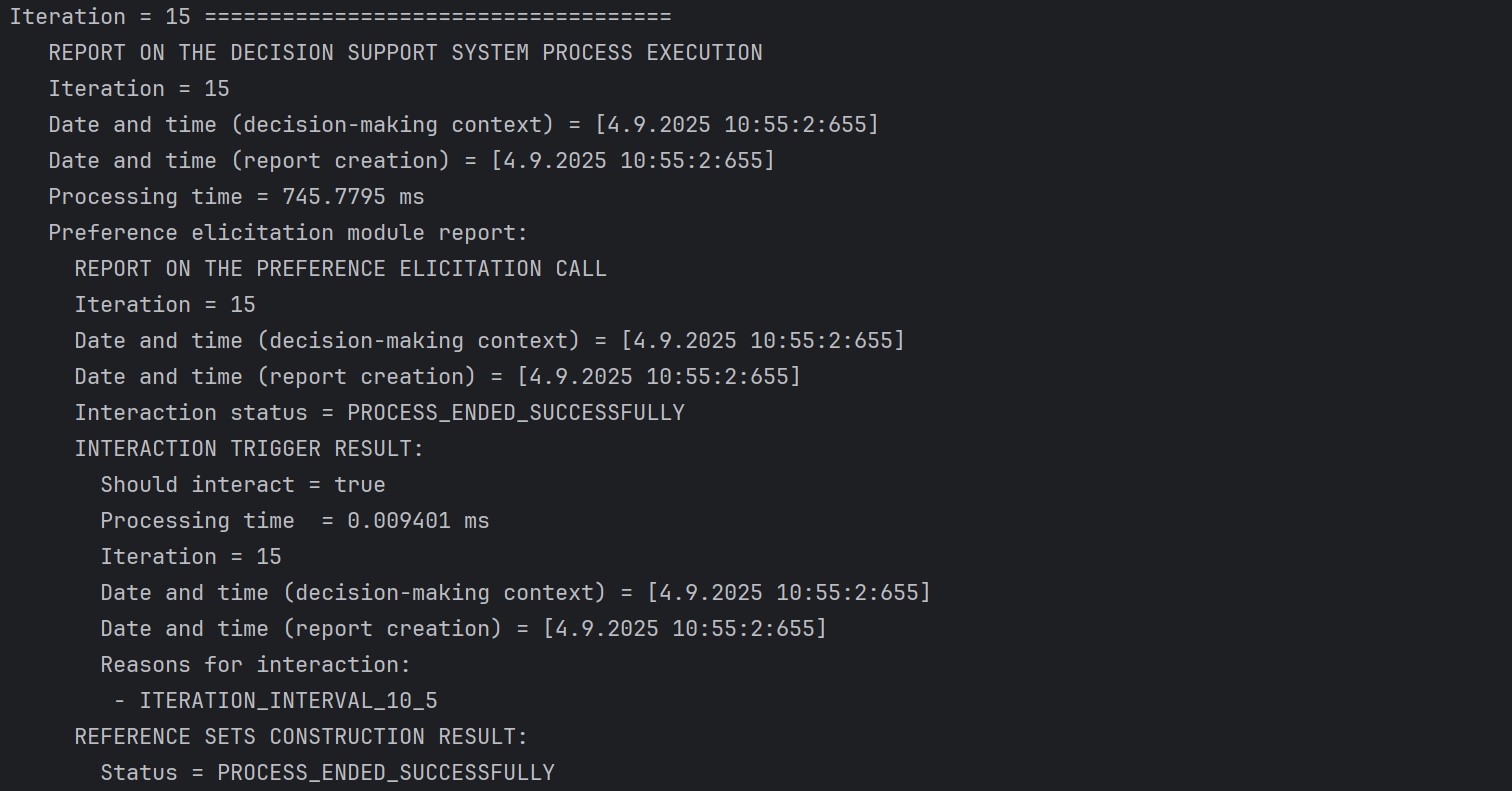
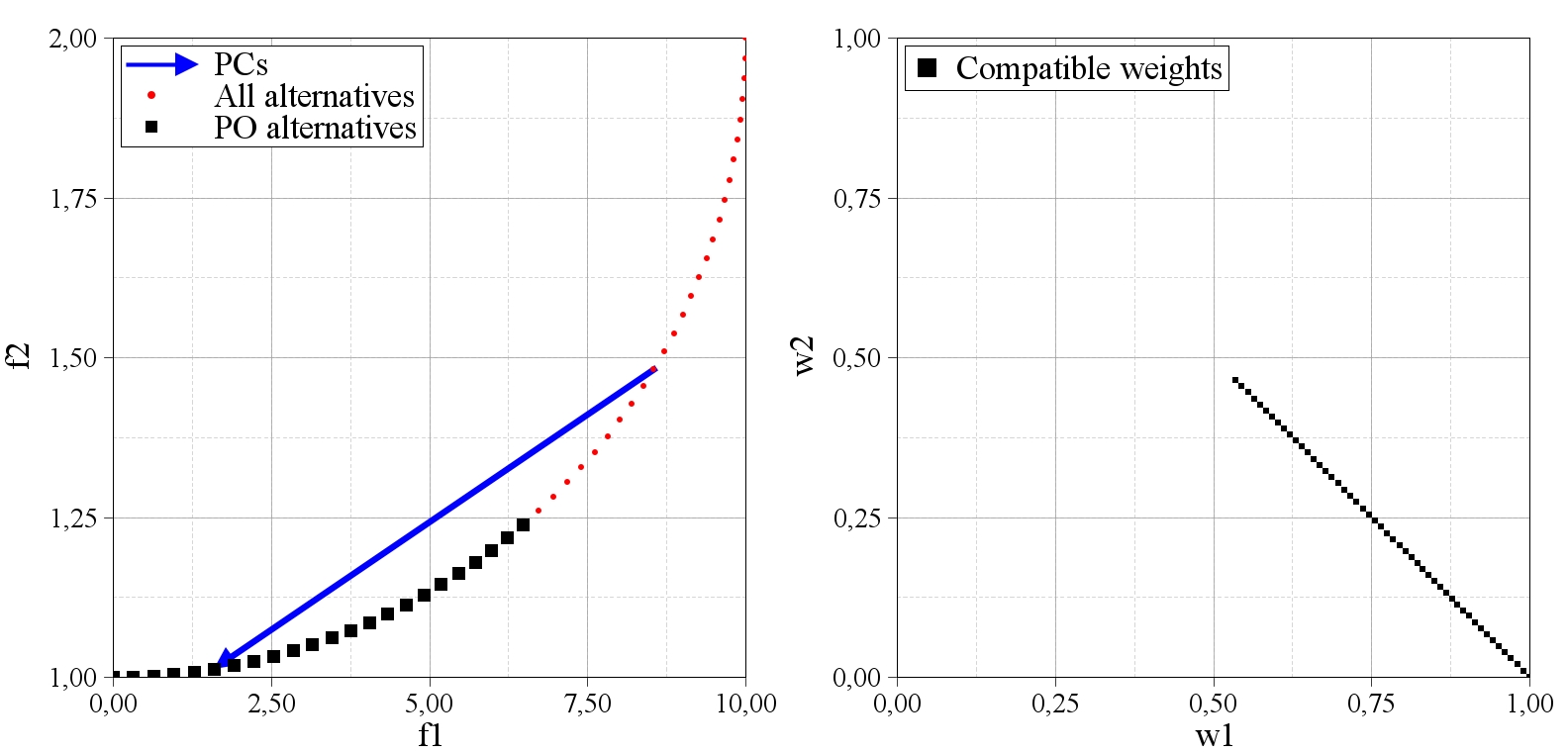
Expected render generated in the 10th iteration:
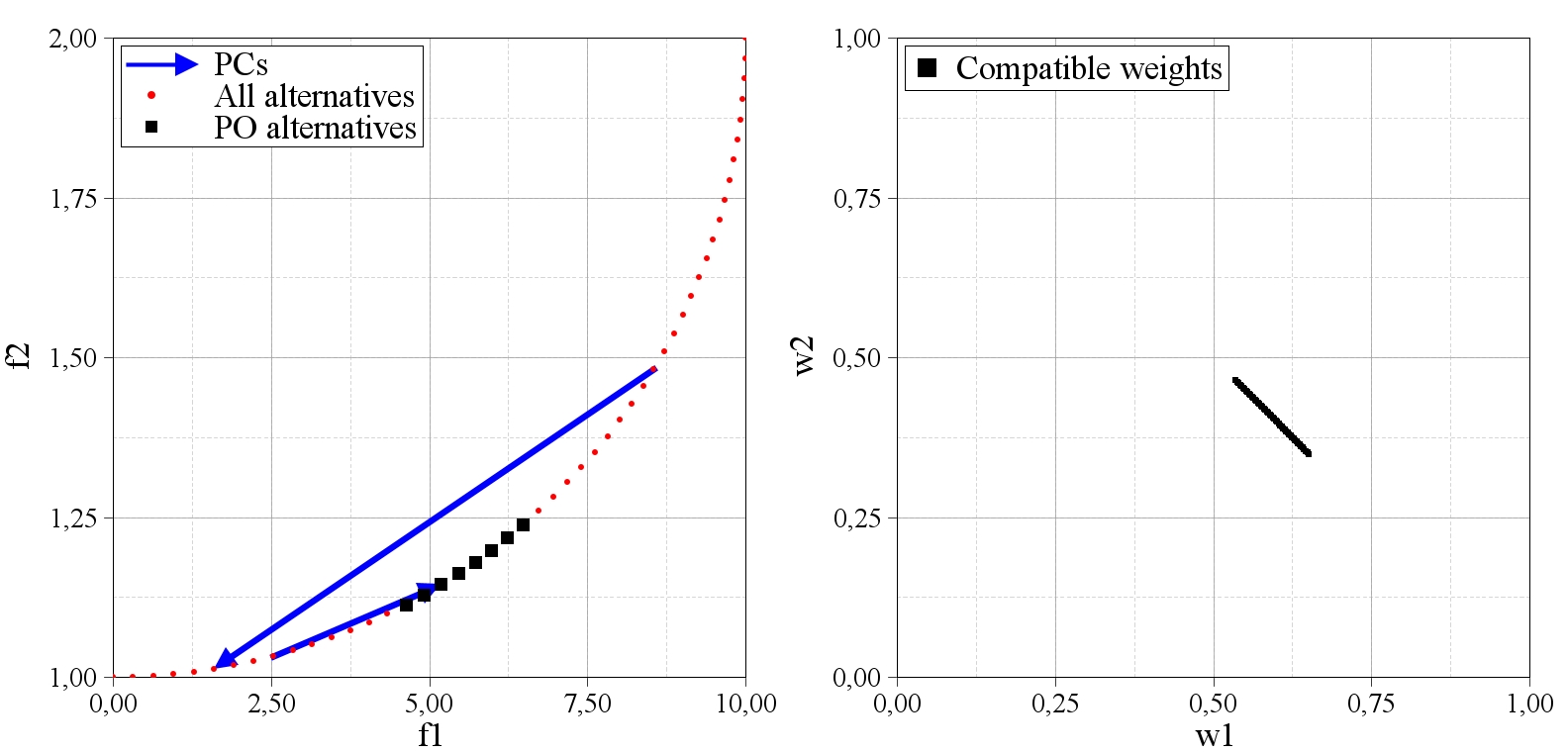
Expected render generated in the 15th iteration:
Used imports:
import alternative.AbstractAlternatives;
import alternative.Alternative;
import alternative.Alternatives;
import color.Color;
import criterion.Criteria;
import dataset.DSFactory2D;
import dataset.IDataSet;
import dataset.painter.style.ArrowStyle;
import dataset.painter.style.ArrowStyles;
import dataset.painter.style.LineStyle;
import dataset.painter.style.MarkerStyle;
import dataset.painter.style.enums.Arrow;
import dataset.painter.style.enums.Marker;
import decisionsupport.operators.LNormOnSimplex;
import dmcontext.DMContext;
import drmanager.DRMPFactory;
import exeption.DecisionSupportSystemException;
import exeption.HistoryException;
import exeption.ModelSystemException;
import exeption.PreferenceModelException;
import frame.Frame;
import history.History;
import history.PreferenceInformationWrapper;
import inconsistency.RemoveOldest;
import interaction.Status;
import interaction.feedbackprovider.FeedbackProvider;
import interaction.feedbackprovider.dm.artificial.value.ArtificialValueDM;
import interaction.reference.ReferenceSetsConstructor;
import interaction.reference.constructor.IReferenceSetConstructor;
import interaction.reference.constructor.RandomPairs;
import interaction.refine.Refiner;
import interaction.refine.filters.reduction.RemoveDominated;
import interaction.refine.filters.termination.RequiredSpread;
import interaction.trigger.InteractionTrigger;
import interaction.trigger.rules.IterationInterval;
import model.IPreferenceModel;
import model.constructor.random.LNormGenerator;
import model.constructor.value.rs.ers.ERS;
import model.constructor.value.rs.ers.comparators.MostSimilarWithTieResolving;
import model.constructor.value.rs.ers.evolutionary.EvolutionaryModelConstructor;
import model.constructor.value.rs.ers.evolutionary.Tournament;
import model.constructor.value.rs.iterationslimit.Constant;
import model.evaluator.EvaluationResult;
import model.evaluator.IEvaluator;
import model.internals.AbstractInternalModel;
import model.internals.value.scalarizing.LNorm;
import model.similarity.lnorm.Euclidean;
import plot.AbstractPlot;
import plot.Plot2D;
import plot.Plot2DFactory;
import plotswrapper.GridPlots;
import preference.indirect.PairwiseComparison;
import print.PrintUtils;
import random.IRandom;
import random.L32_X64_MIX;
import relation.PO;
import relation.Relations;
import scheme.enums.ColorFields;
import space.Range;
import space.normalization.INormalization;
import space.normalization.builder.StandardLinearBuilder;
import space.normalization.minmax.Linear;
import space.normalization.minmax.LinearWithFlip;
import space.os.ObjectiveSpace;
import system.ds.DMBundle;
import system.ds.DecisionSupportSystem;
import system.ds.ModelBundle;
import system.ds.Report;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;Code language: CSS (css)